Question

You are creating an open top box with a piece of cardboard that is 16 x 30“. What size of square should be cut out of each corner to create a box with the largest volume?

Answer 1

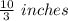`(10)/(3) \ inches` of square should be cut out of each corner to create a box with the largest volume.

Explanation:

Given: Dimension of cardboard= 16 x 30“.

As per the dimension given, we know Lenght is 30 inches and width is 16 inches. Also the cardboard has 4 corners which should be cut out.

Lets assume the cut out size of each corner be "x".

∴ Size of cardboard after 4 corner will be cut out is:

Length (l)=
`30-2x`

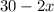
Width (w)=
`16-2x`

Height (h)=
`x`

Now, finding the volume of box after 4 corner been cut out.

Formula; Volume (v)=
`l* w* h`

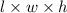
Volume(v)=
`(30-2x)* (16-2x)* x`

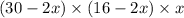
Using distributive property of multiplication

⇒ Volume(v)=
`4x^(3) -92x^(2) +480x`

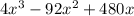
Next using differentiative method to find box largest volume, we will have
`(dv)/(dx)= 0`

`(d (4x^(3) -92x^(2) +480x))/(dx) = (dv)/(dx)`

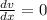
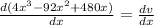
Differentiating the value

⇒
`(dv)/(dx) = 12x^(2) -184x+480`

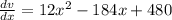
taking out 12 as common in the equation and subtituting the value.

⇒
`0= 12(x^(2) -(46x)/(3) +40)`

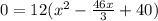
solving quadratic equation inside the parenthesis.

⇒
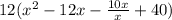`12(x^(2) -12x-(10x)/(x) +40)`=0

Dividing 12 on both side

⇒
`[x(x-12)-(10)/(3) (x-12)]`= 0

We can again take common as (x-12).

⇒
`x(x-12)[x-(10)/(3) ]`=0

∴
`(x-(10)/(3) ) (x-12)= 0`

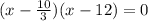
We have two value for x, which is
`12 and (10)/(3)`

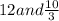
12 is invalid as, w=
`(16-2x)= 16-2* 12`

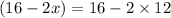
∴ 24 inches can not be cut out of 16 inches width.

Hence, the cut out size from cardboard is
`(10)/(3)\ inches`

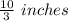
Now, subtituting the value of x to find volume of the box.

Volume(v)=
`(30-2x)* (16-2x)* x`

⇒ Volume(v)=
`(30-2* (10)/(3) )* (16-2* (10)/(3))* (10)/(3)`

⇒ Volume(v)=
`(30-(20)/(3) ) (16-(20)/(3)) ((10)/(3) )`

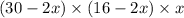
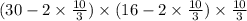
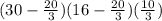
∴ Volume(v)= 725.93 inches³