Answer:
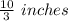 of square should be cut out of each corner to create a box with the largest volume.
of square should be cut out of each corner to create a box with the largest volume.
Explanation:
Given: Dimension of cardboard= 16 x 30“.
As per the dimension given, we know Lenght is 30 inches and width is 16 inches. Also the cardboard has 4 corners which should be cut out.
Lets assume the cut out size of each corner be "x".
∴ Size of cardboard after 4 corner will be cut out is:
Length (l)=
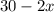
Width (w)=

Height (h)=

Now, finding the volume of box after 4 corner been cut out.
Formula; Volume (v)=
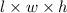
Volume(v)=
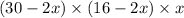
Using distributive property of multiplication
⇒ Volume(v)=
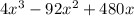
Next using differentiative method to find box largest volume, we will have
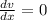

Differentiating the value
⇒

taking out 12 as common in the equation and subtituting the value.
⇒
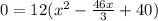
solving quadratic equation inside the parenthesis.
⇒
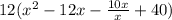 =0
=0
Dividing 12 on both side
⇒
![[x(x-12)-(10)/(3) (x-12)]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/x14ee9jeb1xev7u6gnv40srsg5s4hzw5ln.png) = 0
= 0
We can again take common as (x-12).
⇒
![x(x-12)[x-(10)/(3) ]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/unnlnotx4hx4zxe678xkb6h3xth8p7tmbl.png) =0
=0
∴
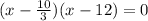
We have two value for x, which is
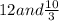
12 is invalid as, w=
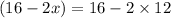
∴ 24 inches can not be cut out of 16 inches width.
Hence, the cut out size from cardboard is
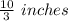
Now, subtituting the value of x to find volume of the box.
Volume(v)=
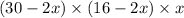
⇒ Volume(v)=
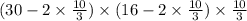
⇒ Volume(v)=
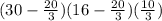
∴ Volume(v)= 725.93 inches³