Answer with Step-by-step explanation:
We are given that
 is an eigenvalue of A.
is an eigenvalue of A.
We have to prove that
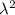 is an eigenvalue of
is an eigenvalue of
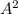
 is eigenvalue of A then, there exist an eigen vector x such that
is eigenvalue of A then, there exist an eigen vector x such that

Multiply by A on both sides then we get
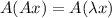
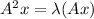
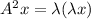

Therefore,
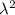 is an eigen value of
is an eigen value of
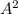
Hence, proved.