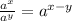Question

Sound Intensity

The relationship between the number of decibles B and the intensity of a sound I (in watts per square centimeter) is given by
β = 10 log10 (I/10^-16).
Find the rate of change in the number of decibles when the intensity is 10-4 watt per square centimeter.

Answer 1

`(d\beta)/(dI)=(10^5)/(ln(10))`

Explanation:

We are given that a relation between the number of decibles B and the intensity of a sound I

`\beta=10log_(10)((I)/(10^(-16)))`

`\beta=10(log_(10)I-(-16)log_(10)10`

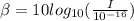
By using property

`log((A)/(B))=log A-log B`

`logA^b=blog A`

`Log_(10)10=1`

`\beta=10(log_(10)I+16)`

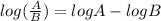
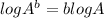
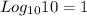
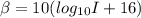
Log 10=1

We have to find the rate of change in the number of decibles when the intensity I=
`10^(-4)watt/cm^2`

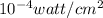
Differentiate w.r.t I

`(d\beta)/(dI)=10((1)/(Iln(10))`

`(d\beta)/(dI)=(10)/(Iln(10))`

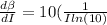
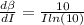
Substitute
`I=10^(-4)`

`(d\beta)/(dI)=(10)/(10^(-4)ln(10))=(10^(1+4))/(ln(10))=(10^5)/(ln(10))`

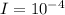
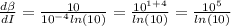
By using property
`(a^x)/(a^y)=a^(x-y)`

`(d\beta)/(dI)=(10^5)/(ln(10))`