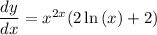Question

Differentiate Functions of Other Bases In Exercise, find the derivative of the function.

y = x2x

Answer 1

`(dy)/(dx) = x^(2x)(2ln(\left (x \right )) + 2)`

Explanation:

Given

`y = x^(2x)`

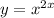
we first need to rewrite this in a form that we know we can differentiate! apply natural log on both sides

`ln((y)) = \ln{(x^(2x))`

`ln((y)) = 2xln((x))`

`y = e^(2xln((x)))`

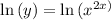
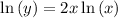
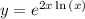
it is to be noted that we two representations of y

`y = e^(2xln((x))) = x^(2x)`

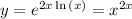
as we know that
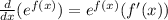`(d)/(dx)(e^(f(x)))=e^(f(x))(f'(x))`, we can use the same rule here.

by using the product rule we can differentiate 2xln(x)

`(dy)/(dx) = e^(2xln((x)))\left((d)/(dx)(2xln((x)))\right)`

`(dy)/(dx) = e^(2xln((x)))(2ln(\left (x \right )) + 2)`

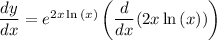
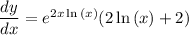
this is our answer and it can also be written as:

`(dy)/(dx) = x^(2x)(2ln(\left (x \right )) + 2)`