Answer:

Explanation:
Given
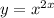
we first need to rewrite this in a form that we know we can differentiate! apply natural log on both sides

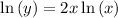
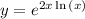
it is to be noted that we two representations of y

as we know that
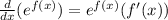 , we can use the same rule here.
, we can use the same rule here.
by using the product rule we can differentiate 2xln(x)
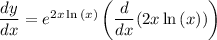
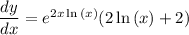
this is our answer and it can also be written as:
