Answer:
Verified
Explanation:
Let the 2x2 matrix A be in the form of:
![\left[\begin{array}{cc}a&b\\c&d\end{array}\right]](https://img.qammunity.org/2021/formulas/mathematics/college/672so31hvv17yja5x20ajbepg9fn7hnrzo.png)
Where det(A) = ad - bc # 0 so A is nonsingular:
Then the transposed version of A is
![A^T = \left[\begin{array}{cc}a&c\\b&d\end{array}\right]](https://img.qammunity.org/2021/formulas/mathematics/college/y4r1vute4edx4pbkddnt4j34o7tn53ngkh.png)
Then the inverted version of transposed A is
![(A^T)^(-1) = (1)/(ad - cb) \left[\begin{array}{cc}a&-c\\-b&d\end{array}\right]](https://img.qammunity.org/2021/formulas/mathematics/college/p1tghacztc0s44dcy9x4me7jgdkab8wawc.png)
The inverted version of A is:
![A^(-1) = (1)/(ad - bc)\left[\begin{array}{cc}a&-b\\-c&d\end{array}\right]](https://img.qammunity.org/2021/formulas/mathematics/college/hszjk1icm7qqjvykpcgk4huhmvs3uirupp.png)
The transposed version of inverted A is:
![(A^(-1))^T = (1)/(ad - bc)\left[\begin{array}{cc}a&-c\\-b&d\end{array}\right]](https://img.qammunity.org/2021/formulas/mathematics/college/nfgvun90f0e6utpnj0hdxmlgn5xzu5rjnn.png)
We can see that
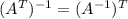
So this theorem is true for 2 x 2 matrices