Question

If A is nonsingular, then (AT )-1 =(A-1) T . (a) Verify this theorem for 2 × 2 matrices

Answer 1

Verified

Explanation:

Let the 2x2 matrix A be in the form of:

`\left[\begin{array}{cc}a&b\\c&d\end{array}\right]`

Where det(A) = ad - bc # 0 so A is nonsingular:

Then the transposed version of A is

`A^T = \left[\begin{array}{cc}a&c\\b&d\end{array}\right]`

Then the inverted version of transposed A is

`(A^T)^(-1) = (1)/(ad - cb) \left[\begin{array}{cc}a&-c\\-b&d\end{array}\right]`

The inverted version of A is:

`A^(-1) = (1)/(ad - bc)\left[\begin{array}{cc}a&-b\\-c&d\end{array}\right]`

The transposed version of inverted A is:

`(A^(-1))^T = (1)/(ad - bc)\left[\begin{array}{cc}a&-c\\-b&d\end{array}\right]`

We can see that

`(A^T)^(-1) = (A^(-1))^T`

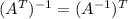
So this theorem is true for 2 x 2 matrices