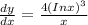Answer:
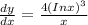
Explanation:
Solving
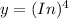
Using function of function (Chain Rule)
 -----(1)
-----(1)
To simplify the function,
Let u = In x
Differentiating u with respect to x
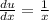 -------- (2)
-------- (2)
Substituting u = In x in the given function
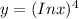
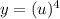
Differentiating y with respect to u

Now that we have
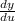 and
and
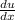 , we can solve for
, we can solve for


Substituting u = In x into the equation,