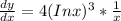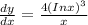Question

Differentiating a Logarithmic Function in Exercise, find the derivative of the function. See Examples 1, 2, 3, and 4.

y = (ln x)4

Answer 1

`(dy)/(dx) = (4(In x)^(3))/(x)`

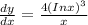
Explanation:

Solving
`y = (In)^(4)`

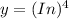
Using function of function (Chain Rule)

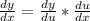`(dy)/(dx) = (dy)/(du) * (du)/(dx)` -----(1)

To simplify the function,

Let u = In x

Differentiating u with respect to x

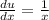`(du)/(dx) = (1)/(x)` -------- (2)

Substituting u = In x in the given function
`y = (In x)^(4)`

`y = (u)^(4)`

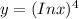
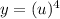
Differentiating y with respect to u

`(dy)/(du) = 4u^(3)`

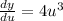
Now that we have
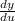`(dy)/(du)` and
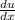`(du)/(dx)`, we can solve for
`(dy)/(dx)`

`(dy)/(dx) = 4u^(3) * (1)/(x)`

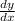
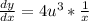
Substituting u = In x into the equation,

`(dy)/(dx) = 4(In x)^(3) * (1)/(x)`

`(dy)/(dx) = (4(In x)^(3))/(x)`