Question

Two resistors of equal value are connected in parallel with each other. The power dissipated by the two resistors will be equal to the ? .

Answer 1

Step-by-step explanation:

Let the two equal resistance be R. the voltage of the source is V.

When the tow resistance are connected in paralel, then the equivalent resistance is R/2 .

Power across this parallel combination

P = 2V²/R

Now when they are connected across the voltage source individually,

P1 = V²/R

P2 = V²/R

So, P = P1 + P2

Thus, the total power is the sum of the individual powers.

Answer 2

Sum of the power dissipated by each resistor connected in parallel.

Solution:

As per the question:

Let the equal value resistor be of R'
`\Omega` each.

In parallel, the equivalent resistance is given by:

`(1)/(R_(e)) = (1)/(R') + (1)/(R')`

`R_(e) = (R'^(2))/(2R') = (R)/(2)`

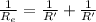
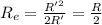
The power dissipated in parallel is given by:

`P_(d) = (V^(2))/(R_(e))`

`P_(d) = (V^(2))/((R)/(2))`

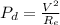
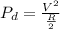
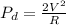`P_(d) = (2V^(2))/(R)` (1)

Also, it can be seen that the overall power dissipated in the resistors is equal to the sum of the power dissipated in each resistor.

Now,

Power dissipated in one resistor, P =
`(V^(2))/(R)`

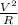
Sum of the power dissipated in each resistor, P =
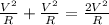`(V^(2))/(R) + (V^(2))/(R) = (2V^(2))/(R)` (2)

Thus from eqn (1) and (2), we can say that the sum of the power in the two resistors connected in parallel is equal.