Question

Condensing Logarithmic Expression In Exercise,use the properties of logarithms to rewrite the expression as the logarithm of a single quantity.See example 4.

4 In x + 6 In y - In z

Answer 1

We can use three rules to solve this logarithm:

Power rule:
`\text{ln}(x^p)=p~\text{ln}(x)`

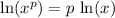
Product rule:
`\text{ln}(xy)=\text{ln}(x)+\text{ln}(y)`

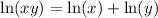
Quotient rule:
`\text{ln}(x)/(y) = \text{ln}(x)-\text{ln}(y)`

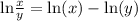
Simplify each part of the logarithm:

4 In x → ln(x^4)

6 In y → ln(y^6)

In z → ln(z)

We multiply ln(x^4) and ln(y^6) according to the product rule and we divide it by ln(z) according to the quotient rule.

Therefore, the logarithm as a single quantity is
`\text{ln}(x^4y^6)/(z)`

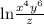
Best of Luck!

Answer 2

In (x^4y^6/z)

Explanation:

4 In x + 6 In y - In z

In x^4 + In y^6 - In z

In (x^4y^6/z)