Question

Inverse Function In Exercise,analytically show that the functions are inverse functions.Then use the graphing utility to show this graphically.

f(x) = e^x - 1
g(x) = In(x + 1)

Answer 1

Explanation:

We need to show whether

`f^(-1)(x) = g(x)`

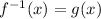
or

`g^(-1)(x) = f(x)`

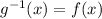
so we'll do either one of them,

we'll convert f(x) to f^-1(x) and lets see if it looks like g(x).

`f(x) = e^x - 1`

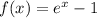
we can also write it as:

`y = e^x - 1`

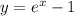
now all we have to do is to make x the subject of the equation.

`y+1 = e^x`

`ln((y+1)) = x`

`x=ln((y+1))`

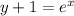
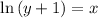
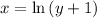
now we'll interchange the variables

`y=ln((x+1))`

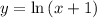
this is the inverse of f(x)

`f^(-1)(x)=ln((x+1))`

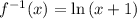
and it does equal to g(x)

`g(x)=ln((x+1))`

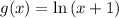
Hence, both functions are inverse of each other!

This can be shown graphically too:

we can see that both functions are reflections of each other about the line y=x.