Incomplete Question the Complete Question is here
Refer to the diagram below. Surveyors know that ∆PQR and ∆STR are similar. What is PQ, the distance across the lake?
3.20 km
3.60 km
2.80 km
3.24 km
Answer:
The Last option is correct 3.24 km
Therefore the distance across the lake is PQ = 3.24 km.
Explanation:
Given:
ΔPQR and ΔSTR are Similar
ST = 1.80 km
TR = 1.25 km
QR = 2.25 km
To Find:
Distance across the lake, PQ = ?
Solution:
ΔPQR ~ ΔSTR ..........Given:
If two triangles are similar then their sides are in proportion.
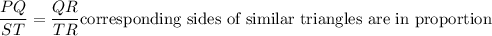
Substituting the values we get
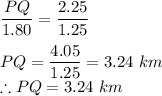
Therefore the distance across the lake is PQ = 3.24 km.