Question

find the angle between the vectors. (first find the exact expression and then approximate to the nearest degree. ) a=[-8,6]. B=[√7, 3]

Answer 1

49°

Explanation:

Given vectors:

a = [-8, 6]

B = [√7, 3]

θ = ?

To find the angle between the two vectors, we will be using the formula,

a.B = |a||B|cosθ

For simplicity, it is good to first calculate the dot product, and the magnitudes. Then we will substitute the values of the dot product, and the magnitudes of the vectors to solve for the angle.

Calculating the dot product

a.B = (-8, 6) . (√7, 3)

= (-8 × √7) + (6 × 3)

= -8√7 + 18

= 18 - 8√7

= 10√7

Calculating the magnitude the vectors

1. The magnitude of vector (-8, 6)

`|a| = \sqrt{(-8)^(2) + 6^(2)}`

`|a| = √(64 + 36)`

`|a| = √(100)`

`|a| = 10`

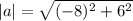
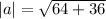
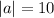
2. The magnitude of vector (√7, 3)

`|B| = \sqrt{(√(7))^(2) + 3^(2)}`

`|B| = √(7 + 9)`

`|B| = √(16)`

`|B| = 4`

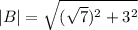
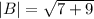
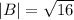
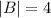
Calculating the angle between the vectors,

cosθ =
`(a.B)/(|a||B|)`

cosθ =
`(10√(7))/(10 * 4)`

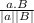
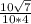
cosθ = 0.6614

θ = cos⁻¹0.6614

θ = 48.59°

θ = 49°