Answer:
Vertex form:
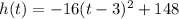
Height expressed as a function of time:
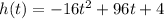
Explanation:
We have been given that the ball is 4 ft above the ground when she hits it.
This means that initial value (y-intercept) of ball is 4.
We are also told that three seconds later it reaches its maximum height of 148 ft. This means
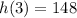 .
.
We know that vertex form of a parabola is in format
 .
.
Let us solve for a using our given information.


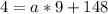
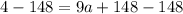
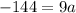


Therefore, the vertex form of our given function would be
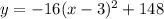 .
.
Since we need height as a function of time, so we will get:
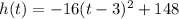
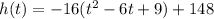
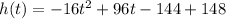
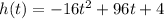
Therefore, the function where height is expressed as a function of time would be
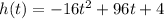 .
.