Answer:

Explanation:
Given:
Parallelogram P is dilated to form parallelogram P'.
The side of P which is = 10 units corresponds 20 units in P'.
The side of P which is given as =(x+3) units corresponds 8 units in P'.
To find the value of
 .
.
Solution:
The scalar factor of dilation from P to P' can be given as the ratio of the corresponding sides of the parallelograms.
The scalar factor :
⇒
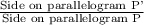
⇒
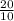
⇒ 2
This means the sides of the parallelogram P' is twice the sides of the parallelogram P.
The side of P which is given as =(x+3) units corresponds 8 units in P'.
Using the scalar factor the equation to solve for
 can be given as:
can be given as:
⇒

Solving for
 .
.
Using distribution:
⇒
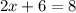
Subtracting both sides by 6.
⇒
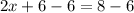
⇒
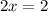
Dividing both sides by 2.
⇒
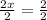
∴
 (Answer)
(Answer)