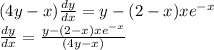Question

Finding Derivatives Implicity In Exercise,Find dy/dx implicity.
x2e - x + 2y2 - xy = 0

Answer 1

the question is incomplete, the complete question is

"Finding Derivatives Implicity In Exercise,Find dy/dx implicity .
`x^(2)e^(-x)+2y^(2)-xy`"

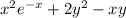Answer :
`(dy)/(dx)=(y-(2-x)xe^(-x))/((4y-x))`

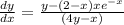
Explanation:

From the expression
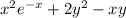`x^(2)e^(-x)+2y^(2)-xy`" y is define as an implicit function of x, hence we differentiate each term of the equation with respect to x.

we arrive at

`(d)/(dx)(x^(2)e^{-x )+(d)/(dx) (2y^(2))-(d)/(dx)xy=0\\`

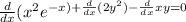
for the expression
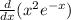`(d)/(dx)(x^(2)e^(-x))` we differentiate using the product rule, also since y^2 is a function of y which itself is a function of x, we have

`(2xe^(-x)-x^(2)e^(-x))+4y(dy)/(dx)-x(dy)/(dx) -y=0\\\\(2-x)xe^(-x)+(4y-x)(dy)/(dx)-y=0 \\`.

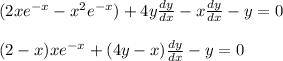if we make dy/dx subject of formula we arrive at

`(4y-x)(dy)/(dx)=y-(2-x)xe^(-x)\\(dy)/(dx)=(y-(2-x)xe^(-x))/((4y-x))`