Question

Which of the following is a solution of y > |x| - 5?
(4, -1)
(-1, -4)
(-4, 1)

Answer 1

(-4, 1) is the solution to given inequality

Solution:

Given inequality is:

y > | x | - 5

The modulus of a real number x, denoted |x|, is the non-negative value of x without regard to its sign

Let us check the options

Option A

Substitute (x, y) = (4, -1) in given inequality and check if it satisfies the inequality

`-1 > | 4 | - 5\\\\-1 > 4 - 5\\\\-1 > -1`

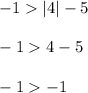
-1 is equal to -1

Thus the inequality is not satisfied

Thus (4, -1) is not the solution

Option B

Substitute (x, y) = (-1, -4) in given inequality

`-4 > | -1 | -5\\\\-4 > 1 - 5\\\\-4 > -4`

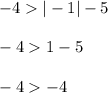
But -4 is equal to -4

So the inequality is not satisfied. Thus (-1, -4) is not a solution

Option C

Substitute (x, y) = (-4, 1) in given inequality

`1 > |-4| - 5\\\\1 > 4 - 5\\\\1 > -1`

1 is greater than -1

Thus the inequality is satisfied

Thus (-4, 1) is the solution