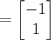Answer:
Eigenvalues : 4 and 2
Eigenvectors : <1,1> and <-1,1>.
Explanation:
The given matrix is
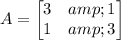
We need to find the eigenvectors and eigenvalues for the matrix.
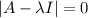
λ represents the eigen values.
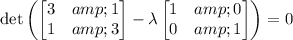
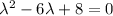
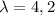
For
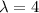
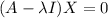
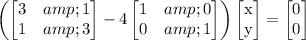
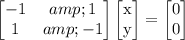
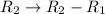
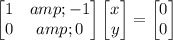
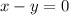
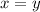
Eigenvector
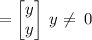
Eigenvector
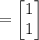
Similarly,
For
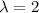
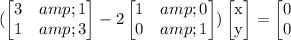
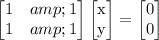
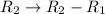
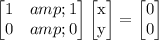
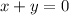
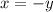
Eigenvector
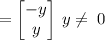
Eigenvector