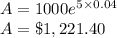Answer:
n = 1, A = $1,216.66
n = 2, A = $1,218.99
n = 4, A = $1,220.1
n = 12, A = $1,221.00
n = 365, A = $1,221.39
Compounded continuously, A = $1,221.40
Explanation:
We are given the following in the question:
P = $1000
r = 4% = 0.04
t = 5 years
The compound interest is given by:
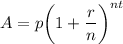
where A is the amount, p is the principal, r is the interest rate, t is the time in years and n is the nature of compound interest.
When compounded continuously:
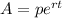
where A is the amount, p is the principal, r is the interest rate, t is the time in years
For n = 1
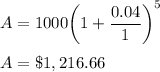
For n = 2
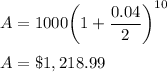
For n = 4
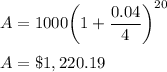
For n = 12
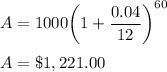
For n = 365
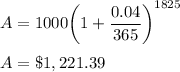
Compounded continuously