Question

Find the value of the integral that converges.
∫^[infinity]_4 ln(5x) dx.

Answer 1

Diverges

Explanation:

We have been given a definite integral
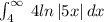`\int _4^(\infty )\:4ln\left|5x\right|dx`. We are asked to determine whether the given integral converges or diverges.

We will use integral by parts formula to solve our given definite integral.

`\int udv=uv-\int vdu`

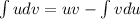
Let
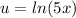`u=ln(5x)` and
`v'=1`.

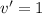Now we need to find du and v using above values.

`(du)/(dx)=(d)/(dx)(ln(5x))`

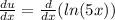
Apply chain rule:

`(du)/(dx)=(1)/(ln(5x))*5=(1)/(x)`

`v'=1`

`v=x`

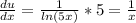
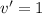
Substitute back these values in parts by integration formula.

`\int _4^(\infty )\:4ln\left|5x\right|dx=4\int _4^(\infty )\:ln\left|5x\right|dx`

`4\int _4^(\infty )\:ln\left|5x\right|dx=4(xln(5x)-\int _4^(\infty )\:x*(1)/(x)dx)`

`4\int _4^(\infty )\:ln\left|5x\right|dx=4(xln(5x)-\int _4^(\infty )\:1dx)`

`4\int _4^(\infty )\:ln\left|5x\right|dx=4(xln(5x)-x)`

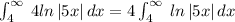
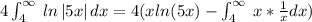
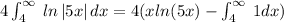
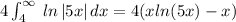
Let us compute the boundaries.

`4(\infty*ln(5(\infty))-\infty)`

`4(4ln(5(4))-4)=31.93171`

`4(\infty*ln(5(\infty))-\infty)-31.93171`

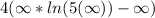
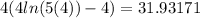
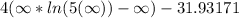
Since
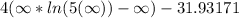`4(\infty*ln(5(\infty))-\infty)-31.93171` is not a finite value, therefore, the integral diverges.