Answer:
5.333 \pi
Explanation:
Given is a function exponential as

The region bounded by the above curve, y =0 , x=4 is rotated about x axis.
The intersection of curve with x axis is at x=0
The limits for x are 0 and 4
The volume when rotated through x axis is found by
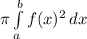
Here a = 0 and b =4
volume =
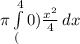
=
