Answer:

Explanation:
Given:
The expression to integrate is given as:
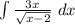
Now, in order to integrate it, we apply the method of substitution.
Let


Differentiating with respect to 't' on both sides, we get:

Replace
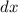 by
by
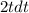 ,
,
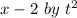 and
and
 by
by
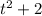 . This gives,
. This gives,
![\int (3(t^2+2))/(√(t^2))\ 2tdt\\\\6\int ((t^2+2)t)/(t)\ dt\\\\6\int (t^2+2)\ dt\\\\6[(t^3)/(3)+2t]+C\\\\2t^3+12t+C](https://img.qammunity.org/2021/formulas/mathematics/college/7cruinan4p6du2szl60lwbdjaynib4ou06.png)
Replacing 't' by
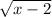 , we get:
, we get:
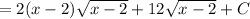

Therefore, the integral is:
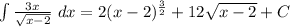
Where 'C' is the constant of integration.