Question

Find the integral, using techniques from this or the previous chapter.
∫x(8-x)3/2 dx

Answer 1

`\int x(8-x)^(3/2)dx= -(16)/(5) (8-x)^{(5)/(2)} +(2)/(7) (8-x)^{(7)/(2)} +C`

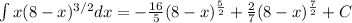
Explanation:

For this case we need to find the following integral:

`\int x(8-x)^(3/2)dx`

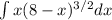
And for this case we can use the substitution
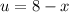`u = 8-x` from here we see that
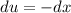`du = -dx`, and if we solve for x we got
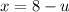`x = 8-u`, so then we can rewrite the integral like this:

`\int x(8-x)^(3/2)dx= \int (8-u) u^(3/2) (-du)`

And if we distribute the exponents we have this:

`\int x(8-x)^(3/2)dx= - \int 8 u^(3/2) + \int u^(5/2) du`

Now we can do the integrals one by one:

`\int x(8-x)^(3/2)dx= -8 (u^(5/2))/((5)/(2)) + (u^(7/2))/((7)/(2)) +C`

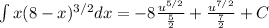
And reordering the terms we have"

`\int x(8-x)^(3/2)dx= -(16)/(5) u^{(5)/(2)} +(2)/(7) u^{(7)/(2)} +C`

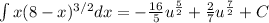
And rewriting in terms of x we got:

`\int x(8-x)^(3/2)dx= -(16)/(5) (8-x)^{(5)/(2)} +(2)/(7) (8-x)^{(7)/(2)} +C`

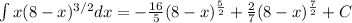
And that would be our final answer.