Question

A publisher reports that 26% of their readers own a laptop. A marketing executive wants to test the claim that the percentage is actually different from the reported percentage. A random sample of 100 found that 17% of the readers owned a laptop. Is there sufficient evidence at the 0.01 level to support the executive's claim?

Answer 1

There is not enough evidence to support the executive's claim that the percentage is actually different from the reported percentage of 26%.

Explanation:

We are given the following in the question:

Sample size, n = 100

p = 26% = 0.26

Alpha, α = 0.01

First, we design the null and the alternate hypothesis

`H_(0): p = 0.26\\H_A: p \\eq 0.26`

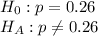
This is a two-tailed test.

Formula:

`\hat{p} = 0.17`

`z = \frac{\hat{p}-p}{\sqrt{(p(1-p))/(n)}}`

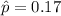
Putting the values, we get,

`z = \displaystyle\frac{0.17-0.26}{\sqrt{(0.26(1-0.26))/(100)}} = -2.051`

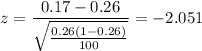
Now, we calculate the p-value from the table.

P-value = 0.040267

Since the p-value is greater than the significance level, we fail to reject the null hypothesis and accept the null hypothesis.

Thus, there is not enough evidence to support the executive's claim that the percentage is actually different from the reported percentage of 26%.