We will solve this problem using the direct concept related to band gap energy, that is, a band gap is the distance between the valence band of electrons and the conduction band, i. e, the energy range in a solid where no electron states (Electronic state) can exist Mathematically can be described as,
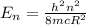
Where,
h = Planck's constant
n = Energy level
mc = Effective mass of the point charge
R = Size of the particle
As you can see the energy is inversely proportional to the size of the particle:
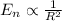
Therefore if the size is decreased, the amount of energy is increased.