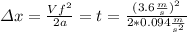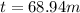Complete question
A 2700 kg car accelerates from rest under the action of two forces. one is a forward force of 1157 newtons provided by traction between the wheels and the road. the other is a 902 newton resistive force due to various frictional forces. how far must the car travel for its speed to reach 3.6 meters per second? answer in units of meters.
Answer:
The car must travel 68.94 meters.
Step-by-step explanation:
First, we are going to find the acceleration of the car using Newton's second Law:
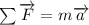 (1)
(1)
with m the mass , a the acceleration and
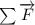 the net force forces that is:
the net force forces that is:
 (2)
(2)
with F the force provided by traction and f the resistive force:
(2) on (1):
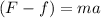
solving for a:
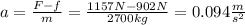
Now let's use the Galileo’s kinematic equation
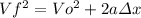 (3)
(3)
With Vo te initial velocity that's zero because it started from rest, Vf the final velocity (3.6) and
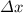 the time took to achieve that velocity, solving (3) for
the time took to achieve that velocity, solving (3) for
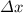 :
: