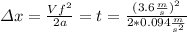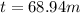Question

The action of two forces. One is a forward force of 1157 N provided by traction between the wheels and the road. The other is a 902 N resistive force due to various frictional forces. How far must the car travel for its speed to reach 3.6 m/s?

Answer 1

Complete question

A 2700 kg car accelerates from rest under the action of two forces. one is a forward force of 1157 newtons provided by traction between the wheels and the road. the other is a 902 newton resistive force due to various frictional forces. how far must the car travel for its speed to reach 3.6 meters per second? answer in units of meters.

Answer:

The car must travel 68.94 meters.

Step-by-step explanation:

First, we are going to find the acceleration of the car using Newton's second Law:

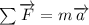`\sum\overrightarrow{F}=m\overrightarrow{a}` (1)

with m the mass , a the acceleration and
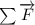`\sum\overrightarrow{F}` the net force forces that is:

`(F-f)` (2)

with F the force provided by traction and f the resistive force:

(2) on (1):

`(F-f)=ma`

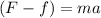
solving for a:

`a=(F-f)/(m) =(1157N-902N)/(2700kg) =0.094(m)/(s^(2))`

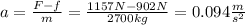
Now let's use the Galileo’s kinematic equation

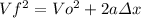`Vf^(2)=Vo^(2)+2a\varDelta x` (3)

With Vo te initial velocity that's zero because it started from rest, Vf the final velocity (3.6) and
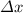`\varDelta x` the time took to achieve that velocity, solving (3) for
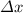`\varDelta x`:

`\varDelta x= (Vf^(2))/(2a) = t= ((3.6(m)/(s))^2)/(2*0.094(m)/(s^(2)))`

`t=68.94 m`