Answer:
a)
Mean of the proportion of clients in this group is 0.07
Standard Deviation of the proportion of clients in the group is 0.018
b)
We need to have at least 10 successes and 10 failures in order to assume the normal approximation. Since n×p=200×0.07>10, the condition is met.
c)
The probability that over 10% of these clients will not make timely payments is 0.05 (5%)
Explanation:
a.Let p be the proportion of the people who receive loans will not make payments on time.
Then p=0.07
Mean of the proportion of clients in this group is 0.07
Standard Deviation of the proportion of clients in the group can be found using the equation:
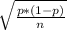 where
where
- p is the proportion of the people who receive loans will not make payments on time. (0.07)
- n is the sample size (200)
Thus
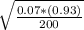 =0.018
=0.018
b.We need to have at least 10 successes and 10 failures in order to assume normal approximation. Since n×p=200×0.07>10, the condition is met.
c.The probability that over 10% of these clients will not make timely payments can be stated as
P(z>z*) where z* is the z-score of p=0.10 in the normal distribution of proportions of the people who receive loans will not make payments on time.
z* can be found using the equation:
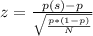 where
where
- N is the sample size (200)
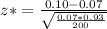 ≈1.663
≈1.663
p-value of z* is ≈0.05
Thus, the probability that over 10% of these clients will not make timely payments is 0.05 (5%)