Question

Loans Based on past experience, a bank believes that 7% of the people who receive loans will not make payments on time. The bank has recently approved 200 loans.

a) What are the mean and standard deviation of the proportion of clients in this group who may not make timely payments?
b) What assumptions underlie your model? Are the conditions met? Explain.
c) What’s the probability that over 10% of these clients will not make timely payments?

Answer 1

a)

Mean of the proportion of clients in this group is 0.07

Standard Deviation of the proportion of clients in the group is 0.018

b)

We need to have at least 10 successes and 10 failures in order to assume the normal approximation. Since n×p=200×0.07>10, the condition is met.

c)

The probability that over 10% of these clients will not make timely payments is 0.05 (5%)

Explanation:

a.Let p be the proportion of the people who receive loans will not make payments on time.

Then p=0.07

Mean of the proportion of clients in this group is 0.07

Standard Deviation of the proportion of clients in the group can be found using the equation:

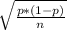`\sqrt{(p*(1-p))/(n) }` where

• p is the proportion of the people who receive loans will not make payments on time. (0.07)

• n is the sample size (200)

Thus
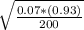`\sqrt{(0.07*(0.93))/(200) }` =0.018

b.We need to have at least 10 successes and 10 failures in order to assume normal approximation. Since n×p=200×0.07>10, the condition is met.

c.The probability that over 10% of these clients will not make timely payments can be stated as

P(z>z*) where z* is the z-score of p=0.10 in the normal distribution of proportions of the people who receive loans will not make payments on time.

z* can be found using the equation:

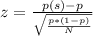`z=\frac{p(s)-p}{\sqrt{(p*(1-p))/(N) } }` where

• p(s)=0.10

• p =0.07

• N is the sample size (200)

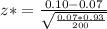`z*=\frac{0.10-0.07}{\sqrt{(0.07*0.93)/(200) } }` ≈1.663

p-value of z* is ≈0.05

Thus, the probability that over 10% of these clients will not make timely payments is 0.05 (5%)

Answer 2

a)
`\mu_p = 0.07`

`\sigma_p =\sqrt{(0.07(1-0.07))/(200)}=0.018`

b) 1) Independence between the loans recieved

2) We are asuming that the sample size of 200 is less than 10% of the total loans

3) np = 200*0.7 = 14>10

n(1-p)= 200*(1-0.07) = 186>10

c)
`P(p>0.1)=P((X-\mu)/(\sigma)>(0.1-\mu_p)/(\sigma_p))=P(Z>(0.1-0.07)/(0.018))=P(Z>1.67)`

And we can find this probability on this way:

`P(Z>1.67)=1-P(Z<1.67)= 1-0.953=0.047`

Explanation:

Part a

For this case we know that the population proportion is given by:

`p \sim N(p, \sqrt{(p(1-p))/(n)})`

So then:

`\mu_p = 0.07`

`\sigma_p =\sqrt{(0.07(1-0.07))/(200)}=0.018`

Part b

For this case we are assuming the following 3 conditions:

1) Independence between the loans recieved

2) We are asuming that the sample size of 200 is less than 10% of the total loans

3) np = 200*0.7 = 14>10

n(1-p)= 200*(1-0.07) = 186>10

Part 3

We are interested on this probability

`P(p>0.1)`

And the best way to solve this problem is using the normal standard distribution and the z score given by:

`z=(x-\mu)/(\sigma)`

If we apply this formula to our probability we got this:

`P(p>0.1)=P((X-\mu)/(\sigma)>(0.1-\mu_p)/(\sigma_p))=P(Z>(0.1-0.07)/(0.018))=P(Z>1.67)`

And we can find this probability on this way:

`P(Z>1.67)=1-P(Z<1.67)= 1-0.953=0.047`