Question

One day in March in Hilton Head, South Carolina, the first high tide occurred at 6:18 A.M. The high tide was 7.05 feet, and the low tide was -0.30 feet. The period for the oscillation of the tides is 12 hours and 24 minutes.

a. Determine what time the next high tide will occur.
b. Write the period of the oscillation as a decimal.
c. What is the amplitude of the sinusoidal function that models the tide?
d. If t 0 represents midnight, write a sinusoidal function that models the tide.
e. At what time will the tides be at 6 feet for the first time that day?

Answer 1

A. The next high tide occurs at 6:42 P.M.

B. The period T is 12.4 hs.

C. The amplitude of the oscillation is 3.675 feet.

D. The function is of the form
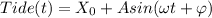`Tide(t)=X_(0)+Asin(\omega t+\varphi)`, with t in hours. This function is:

`Tide(t)=3.375feet+(3.675 feet)sin(0.5067(1)/(hs) t-1.621rad)`

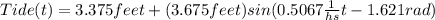
E. The tide will reach 6 feet for first time at 4:16 A.M.

Step-by-step explanation:

A. The high tide will repeat itself after a full period, which is 12:24 hours. That means that the next high tide will occur at t=6:18hs+12:24hs=18:42hs=6:42P.M.

B. For the periode we can use a direct Rule of Three:

60 min ↔ 1h

24 min ↔ x=24/60=0.4 ⇒ T=12.4hs

C. Amplitud and initial hight can be obtain as:

`A=(X_(max)-X_(min))/(2)=(7.05feet-(-0.3feet))/(2)=3.675feet`

`X_(0)=A+X_(min)=3.675feet-0.3feet=3.375feet`

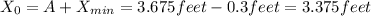
D. As said above, the function is of the form
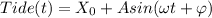`Tide(t)=X_(0)+Asin(\omega t+\varphi)`, with t in hours. With this form:

`\omega=(2\pi)/(T)= (2\pi)/(12.4hs)=(0.5067rad)/(hs)`

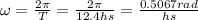
The maximum tide happens when the sin(X)=1 ↔ αmax=π/2.

`\alpha_(max)=(\pi)/(2) Rad=\omega t_(max)+\varphi\\\varphi=(\pi)/(2) Rad-(0.5067rad)/(hs)6.3hs=-1.621rad`

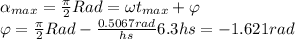
E. To know the time at wich the tide will be 6 feet, we introduce that data in the function:

`Tide(t)=6feet=3.375feet+(3.675 feet)sin(0.5067(1)/(hs) t-1.621rad)\\(5)/(7)=sin(0.5067(1)/(hs) t-1.621rad)\\Arcsin((5)/(7))+1.621rad=0.5067(1)/(hs)t\\t=4.77hs\approx4:16hs`