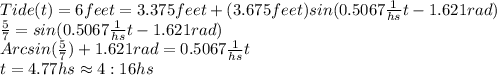Answer:
A. The next high tide occurs at 6:42 P.M.
B. The period T is 12.4 hs.
C. The amplitude of the oscillation is 3.675 feet.
D. The function is of the form
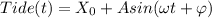 , with t in hours. This function is:
, with t in hours. This function is:
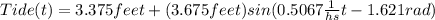
E. The tide will reach 6 feet for first time at 4:16 A.M.
Step-by-step explanation:
A. The high tide will repeat itself after a full period, which is 12:24 hours. That means that the next high tide will occur at t=6:18hs+12:24hs=18:42hs=6:42P.M.
B. For the periode we can use a direct Rule of Three:
60 min ↔ 1h
24 min ↔ x=24/60=0.4 ⇒ T=12.4hs
C. Amplitud and initial hight can be obtain as:
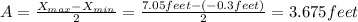
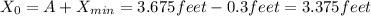
D. As said above, the function is of the form
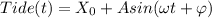 , with t in hours. With this form:
, with t in hours. With this form:
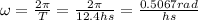
The maximum tide happens when the sin(X)=1 ↔ αmax=π/2.
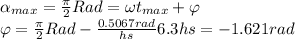
E. To know the time at wich the tide will be 6 feet, we introduce that data in the function: