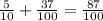The expression is:
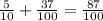
Solution:
Given that we have to find:
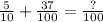
Let the unknown be "x"
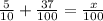
Let us solve the above expression to find for "x"
We have to solve the left hand side of expression
Make the denominators of left hand side same for easier calculations
We have to take L.C.M of 10 and 100
L.C.M of 10 and 100:
List all prime factors for each number
Prime Factorization of 10 is: 2 x 5
Prime Factorization of 100 is: 2 x 2 x 5 x 5
For each prime factor, find where it occurs most often as a factor and write it that many times in a new list.
The new superset list is
2, 2, 5, 5
Multiply these factors together to find the LCM.
LCM = 2 x 2 x 5 x 5 = 100
Now divide the numerator and denominator by a number so that denominator becomes 100
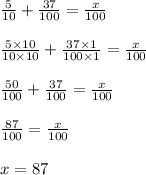
Thus the expression is: