Question

The speed of a moving bullet can be determined by allowing the bullet to pass through two rotating paper disks mounted a distance 64 cm apart on the same axle. From the angular displacement 20.3 ◦ of the two bullet holes in the disks and the rotational speed 1165 rev/min of the disks, we can determine the speed of the bullet.Find the bullet speed.

Answer 1

The speed of the bullet is 220.6 m/s.

Step-by-step explanation:

Given that,

Distance = 64 cm

Angular displacement = 20.3°

Rotational speed = 1165 rev/min

We need to calculate the time

Using formula of angular displacement

`\theta=\omega* t`

`t=(\theta)/(\omega)`

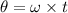
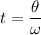
Put the value into the formula

`t=(20.3*(\pi)/(180))/(1165*(2\pi)/(60))`

`t=0.00290\ sec`

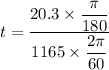
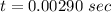
We need to calculate the speed of the bullet

Using formula of speed

`v=(d)/(t)`

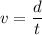
Put the value into the formula

`v=(64*10^(-2))/(0.00290)`

`v=220.6\ m/s`

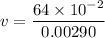
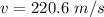
Hence, The speed of the bullet is 220.6 m/s.