Question

Suppose astronomers built a 20-meter telescope. How much greater would its light-collecting area be than that of the 10-meter Keck telescope?

Answer 1

4 times greater

Step-by-step explanation:

Step 1: Calculate light-collecting area of a 20-meter telescope (A₁) by using area of a circle.

Area of circle = π*r² =
`(\pi d^(2))/(4)`

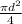
Where d is the diameter of the circle = 20-m

`A_(1) = (\pi d^(2))/(4)`

`A_(1) = (\pi (20^(2)))/(4)`

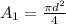
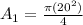
A₁ = 314.2 m²

Step 2: Calculate light-collecting area of a 10-meter Keck telescope (A₂)

`A_(2) = (\pi d^(2))/(4)`

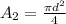
Where d is the diameter of the circle = 10-m

`A_(2) = (\pi (10^(2)))/(4)`

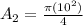
A₂ = 78.55 m²

Step 3: divide A₁ by A₂

`= (314.2 m^2)/(78.55 m^2)`

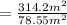
= 4

Therefor, the 20-meter telescope light-collecting area would be 4 times greater than that of the 10-meter Keck telescope.