Question

A running mountain lion can make a leap 10.0 mlong, reaching a maximum height of 3.0 m. What is the speed of the mountain lion just as it leaves the ground? At what angle does it leave the ground?

Answer 1

To solve this problem we will use the kinematic equations of descriptive motion of a projectile for which both the height reached and the distance traveled are defined. From this type of movement the lion reaches a height (H) of 3m and travels a horizontal distance (R) of 10 m. Mathematically the equations that describe this movement are given as,

`H = (v_0^2sin^2\theta)/(2g)`

`R = (v_0^2 sin 2\theta)/(g)`

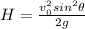
Dividing the two equation we have that

`(H)/(R)=((v_0^2sin^2\theta)/(2g))/((v_0^2 sin 2\theta)/(g))`

`(H)/(R)= (sin^2\theta)/(2)*(1)/(sin2\theta)`

`(H)/(R)= (sin^2\theta)/(2)*(1)/(2sin\theta cos\theta)`

`(H)/(R)= (1)/(4) (sin\theta)/(cos\theta)`

`(H)/(R)= (1)/(4) tan\theta`

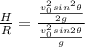
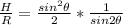
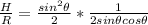
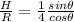
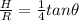
Substituting values of H and R, we get

`(3)/(10) = (1)/(4) tan\theta`

`\theta = tan^(-1) (12)/(10)`

`\theta = 50.2\°`

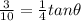
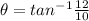
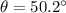
Substituting the value of \theta in equation we get,

`H = (v_0^2sin^2\theta)/(2g)`

`v_0^2 = (H 2g)/(sin^2\theta)`

`v_0^2 = (3*2*9.8)/(sin^2(50.2))`

`v_0^2 = 99.62`

`v_0 = √(99.62)`

`v_0 = 9.98m/s`

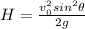
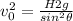
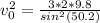
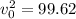
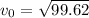
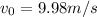
Therefore the speed of the mountain lion just as it leaves the ground is 9.98m/s at an angle of 50.2°