1140 ways are there to select three person subcommittee from a club of twenty students
Solution:
Given that a club of twenty students wants to pick a three person subcommittee
To find: number of ways this can be done
We have to use combinations formula to solve the given sum
A combination is a selection of all or part of a set of objects, without regard to the order in which objects are selected
The formula to calculate combinations is:
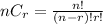
where n represents the number of items, and r represents the number of items being chosen at a time
Here we have to choose 3 persons from 20 students
So, n = 20 and r = 3
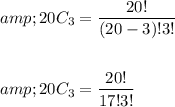
To get the factorial of a number n ,the given formula is used,
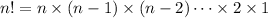
Therefore,
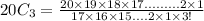
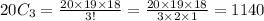
Thus 1140 ways are there to select three person subcommittee from a club of twenty students