Answer:
Explanation:
4x + y = 8
x + 3y = 8
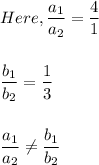
So, this system of equations is consistent and independent.
-4x + 6y = -2
2x - 3y = 1
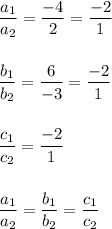
So, the system of linear equations are consistent and dependent.
5x -2y = 4
5x - 2y = 6
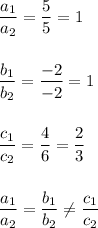
This system of equations is inconsistent.