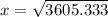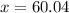Question

An equilateral triangle has a height of 52 cm. Determine the length of

each side to the nearest hundredth of a centimeter.

Answer 1

`60.04\ cm`

Explanation:

Let

a ----> the length of each side

we know that

Applying the Pythagorean Theorem

`a^2=h^2+(a/2)^2`

solve for a

`a^2-(a/2)^2=h^2`

`(3/4)a^2=h^2`

`a^2=(4/3)h^2`

`a^2=(4/3)(52)^2`

`a=60.04\ cm`

Answer 2

60.04 cm

Explanation:

Let the sides of the equilateral triangle be
`x\: cm`

The equilateral triangle has a height of 52 cm.

From the diagram in the attachment, we can apply the Pythagoras Theorem to obtain:

`x^2=52^2+((x)/(2))^2`

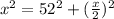
This implies that:

`x^2=52^2+(x^2)/(4)`

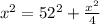
We multiply through by 4 to get:

`4x^2=10816+x^2`

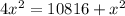
Group similar terms to get:

`4x^2- x^2=10816`

`3x^2=10816`

`x^2=3605.333`

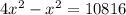
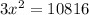
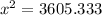
Take square root to get:

`x=√(3605.333)`

`x=60.04`