Question

- Write a recursive formula to represent the sequence below.

(3,7, 11, 15, 19,23,27,31,35, ...)

Answer 1

The recursive formula to find nth term of sequence is:

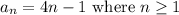`a_n = 4n - 1 \text{ where } n \geq 1` and n = 1, 2, 3, ....

Solution:

Given a sequence is:

3, 7, 11, 15, 19, 23, 27, 31, 35

Let us find the difference between terms

7 - 3 = 4

11 - 7 = 4

15 - 11 = 4

19 - 15 = 4

23 - 19 = 4

27 - 23 = 4

31 - 27 = 4

35 - 31 = 4

Thus the difference between terms is constant

Thus the given sequence is arithmetic sequence

An arithmetic sequence is a sequence of numbers such that the difference of any two successive members of the sequence is a constant

The nth term of arithmetic sequence is given by:

`a_n =a_1+(n-1)d`

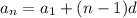
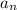`a_n` = the nᵗʰ term in the sequence

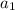`a_1` = the first term in the sequence

d = the common difference between terms

Here in the given sequence

d = 4

`a_1=3`

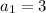
Substitute in above formula,

`a_n = 3 + (n-1)(4)\\\\a_n = 3 + 4n - 4\\\\a_n = 4n - 1`

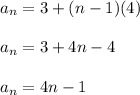
Thus the recursive formula to find nth term of sequence is:

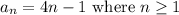`a_n = 4n - 1 \text{ where } n \geq 1` and n = 1, 2, 3, ......