The recursive formula to find nth term of sequence is:
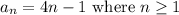 and n = 1, 2, 3, ....
and n = 1, 2, 3, ....
Solution:
Given a sequence is:
3, 7, 11, 15, 19, 23, 27, 31, 35
Let us find the difference between terms
7 - 3 = 4
11 - 7 = 4
15 - 11 = 4
19 - 15 = 4
23 - 19 = 4
27 - 23 = 4
31 - 27 = 4
35 - 31 = 4
Thus the difference between terms is constant
Thus the given sequence is arithmetic sequence
An arithmetic sequence is a sequence of numbers such that the difference of any two successive members of the sequence is a constant
The nth term of arithmetic sequence is given by:
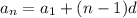
 = the nᵗʰ term in the sequence
= the nᵗʰ term in the sequence
 = the first term in the sequence
= the first term in the sequence
d = the common difference between terms
Here in the given sequence
d = 4
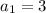
Substitute in above formula,
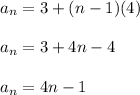
Thus the recursive formula to find nth term of sequence is:
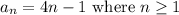 and n = 1, 2, 3, ......
and n = 1, 2, 3, ......