Answer:
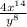
Explanation:
We have tthe following expression:
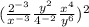
Firstly, we have to solve the oeprations inside the parenthesis. Let's begin by grouping similar coefficients:

Rewriting the expression:
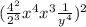
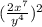
Multiplying the exponent outside the parenthesis with the exponents inside:
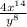 This is the final result
This is the final result