Question

In Triangle PQR, the measure of ZR=90°, the measure of ZP=51°, and QR = 38 feet. Find the length of PQ to the nearest tenth of a foot.

Answer 1

Therefore Length of PQ is 48.9 foot.

Explanation:

Given:

In Triangle PQR,

∠R = 90°

∠P = 51°

QR = 38 feet = side opposite to angle P

To Find:

PQ = ? = Hypotenuse

Solution:

In Right angle Triangle PQR Cosine Identity we get,

`\sin P = \frac{\textrm{side opposite to angle P}}{Hypotenuse}\\`

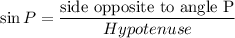
Substituting the values we get,

`\sin 51 = (QR)/(PQ)=(38)/(PQ)\\\\0.7771=(38)/(PQ)\\\\PQ=(38)/(0.7771)=48.899\\\\\therefore PQ=48.9\ foot`

Therefore Length of PQ is 48.9 foot.