Question

1. Write the equation in slope intercept form for the line that is perpendicular to the line passing through

(-6, 2) and (-4,-3) and passes through the point (2,-5) and then graph the perpendicular line and the
original line. Show all work.

Answer 1

y=2x-9

Explanation:

First, find the slope of the original line.

The slope ends up as 1/2. Then, take the opposite and plug into a point-slope equaion using the opposite slope (2/1) and the point the new line will pass through (2,-5). Simplify and graph.

Answer 2

The answer to your question is y = 2/5 x - 29/5

Explanation:

Data

Points of the first line

A (-6, 2)

B (-4, -3)

Points of the second line

C (2, 5)

Process

1.- Find the slope of the first line

`m = (y2 - y1)/(x2 - x1)`

`m = (-3 - 2)/(-4 + 6) = (-5)/(2)`

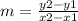
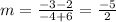
Original line

y - 2 = -5/2 (x + 6)

y = -5/2 x - 15 + 2

y = -5/2 x - 13

2.- Find the slope of the new line, if the lines are perpendicular,

m =
`(2)/(5)`

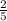
3.- Find the equation of the line

y - y1 = m(x - x1)

Substitution

y + 5 = 2/5(x - 2)

Simplification and result

y = 2/5x - 4/5 - 5

y = 2/5 x - 4/5 - 25/5

y = 2/5 x - 29/5