Answer:
ΔT ∝
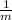
Step-by-step explanation:
We know that, the heat input to a body is given as:
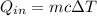
Where,

Specific heat capacity of a body depends on its material and thus is constant for a given body.
Rewriting the above equation in terms of
 , we get:
, we get:

Now, as per given question, the heat supply to the given body is a constant.
Therefore, replacing the constant quantities by a constant 'K', we get:
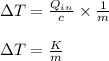
So, rise in temperature is a function of the mass only and varies inversely with the mass.
⇒ ΔT ∝
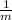
Therefore, the temperature rise of a body is INVERSELY PROPORTIONAL to its mass for the same heat energy input.