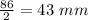Distance between top of a crest and bottom of a trough for the transverse water wave = 96 mm
Length of the trough = 43 mm
Step-by-step explanation:
Consider a transverse wave as shown in the attached figure. Given:
Amplitude = A = 48 mm
Wavelength = λ = 86 mm
For a transverse wave, the distance between the crest and equilibrium position is equal to the distance between the trough and the equilibrium position. This distance is termed as the amplitude. ..............(1)
Amplitude = 48 mm
(Refer attached figure.) The vertical displacement between the top of a crest and bottom of a trough is the distance between C and T.
This distance is equal to two times the amplitude. (From (1))
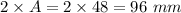
Distance between top of a crest and bottom of a trough = 96 mm
Total wavelength of a transverse wave (λ) = Length of crest + Length of trough
For a transverse wave, Length of crest = Length of trough = x
Since λ = 2x, x = λ/2.
Therefore length of the trough = λ/2 =