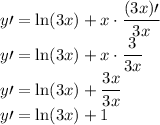Question

Differentiate y=xln(3x)​

Answer 1

`\displaystyle \large{y\prime = \ln (3x)+1}`

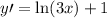
Explanation:

Hi! To differentiate the function given, notice that there are two functions multiplying each other which are x and ln(3x).

Since there are two functions multiplying each other, we will have to use the product rules:

`\displaystyle \large{y = f(x)g(x) \to y\prime = f\prime (x)g(x) + f(x)g\prime (x)}`

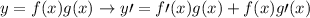
That means we have
`\displaystyle \large{y\prime = (x)\prime \ln (3x) + x[ln(3x)]\prime` - the ‘ symbol means to be differentiated and it’s called prime.

Recall the power rules for polynomial and natural logarithm differentiation.

Note that the differentiation rules below also apply chain rules where “u” is another function other than “x”.

`\displaystyle \large {(u^n)\prime = nu^(n-1) \cdot u\prime}\\\displaystyle \large{(\ln |u|)\prime = (1)/(u) \cdot u\prime \to (u\prime)/(u)`

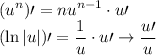
Therefore:

`\displaystyle \large{y\prime = \ln (3x) + x\cdot ((3x)\prime)/(3x)}\\\displaystyle \large{y\prime = \ln (3x) + x\cdot (3)/(3x)}\\\displaystyle \large{y\prime = \ln (3x) + (3x)/(3x)}\\\displaystyle \large{y\prime = \ln (3x) + 1}`