Question

The graph of f(x) is shown below.

If f(x) and its inverse function, f^-1 (x), are both plotted on the same coordinate plane, where is their point of intersection?​

Answer 1

Its is C. on edg....(2,2)

Explanation:

got it correct :D 2022

Answer 2

(2,2)

Explanation:

1. Find the equation of the function f(x). The graph of this function passes through the points (3,0) and (0,6). Then its equation is

`y-6=(0-6)/(3-0)(x-0)\\ \\y-6=-2x\\ \\y=-2x+6`

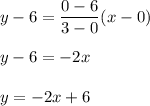
2. Find the equation of the inverse function
`f^(-1)(x):`

`y=-2x+6\\ \\y-6=-2x\\ \\x=-(1)/(2)(y-6)\\ \\x=-(1)/(2)y+3`

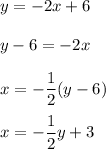
Change x into y and y into x:

`y=-(1)/(2)x+3`

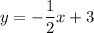
3. Find the point of intersection solving the system of two equations:

`\left\{\begin{array}{l}y=-2x+6\\ \\y=-(1)/(2)x+3\end{array}\right.`

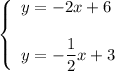
Equate right parts:

`-2x+6=-(1)/(2)x+3\\ \\-4x+12=-x+6\\ \\-4x+x=6-12\\ \\-3x=-6\\ \\x=2\\ \\y=-2\cdot 2+6=2`

Hence, the point of intersection has coordinates (2,2)