Question

Prove that tan^2A + cot^2A = 1 is not a trigonometric identity by producing a counterexample​

Answer 1

the guy above is 100% correct

Explanation:

Answer 2

Proof is given below.

`tan^2 45\°+cot^2 45\° \\e 1`

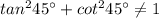
Explanation:

To prove:
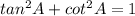`tan^2 A+cot^2 A = 1` is not a trigonometric identity.

A trigonometric identity is an equation whose left hand side is always to the right hand side for any value of the given angle.

A counterexample is a method used to counter the given statement by taking a random value for the given quantity and disproving the left and right side of the equation.

So, let us take A = 45°

Then, left hand side of the equation becomes;

`tan^2 45\°+cot^2 45\°=(1)^2 +(1)^2=1+1=2`

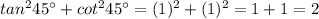
Therefore, the value of left hand side of the equation on plugging in 45° for A gives the result as 2.

But the right hand side of the equation is equal to 1.

Therefore,
`tan^2 45\°+cot^2 45\° \\e 1`

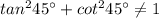
So, this violates the given equation and hence the given equation is not always true. So, it's not a trigonometric identity.